 PDF version of this document
PDF version of this document
Let us assume that we were given a set of ![]() images
images
![]() .
Each of these images is two-dimensional - in the simpler case at
least. An image is
.
Each of these images is two-dimensional - in the simpler case at
least. An image is ![]() pixels nigh and
pixels nigh and ![]() pixels wide. Each perturbation
(displacement)
pixels wide. Each perturbation
(displacement) ![]() has a direction
has a direction
![]() and an intensity (vector length) associated with it. Let us define
the total displacement to be
and an intensity (vector length) associated with it. Let us define
the total displacement to be
![]() and the average
and the average
![]() accordingly. Then,
accordingly. Then,
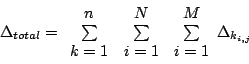 |
(1) |
and
| (2) |
Having formulated it in this way, a more proper average should treat
the displacements in each image separately and not aggregate displacements
in each of the ![]() images.
images.
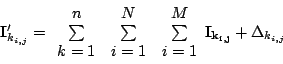 |
(3) |
only reflects on how the new set of images are generated. Rather than calculating a sum, it forms a set of matrices (in a vector-wise assignment).
Some displacement
![]() has been applied to each of
the pixels,
has been applied to each of
the pixels,
![]() in each of of the images in the
set. We seek a way of selecting
in each of of the images in the
set. We seek a way of selecting ![]() in a way which obeys certain
rules. The goal is the obtain a stack whose members are the images
in a way which obeys certain
rules. The goal is the obtain a stack whose members are the images
![]() and where each
member of the stack has an increasing amount of displacement applied.
The perturbation method needs to sensibly pick values for
and where each
member of the stack has an increasing amount of displacement applied.
The perturbation method needs to sensibly pick values for
![]() so that a clear relationship among stack member should emerge.
so that a clear relationship among stack member should emerge.