


Next: Results
Up: Normalisation Experiments: Planning, Deployment,
Previous: Normalisation Experiments: Planning, Deployment,
S everal experiments that fall under the same theme
have already been run. They are summarised in a weekly progress1. Below we have listed a list of experiments whose educational value
justifies systematic variation of one parameter or another.
- Varying
 : Does one get the same behaviour when changing
from a Euclidean distance to a shuffle distance? If the variation
as function of set size is linear (i.e. we get a straight line as
before), does it have the expected slope? Do we even get a straight
line at all?
: Does one get the same behaviour when changing
from a Euclidean distance to a shuffle distance? If the variation
as function of set size is linear (i.e. we get a straight line as
before), does it have the expected slope? Do we even get a straight
line at all?
- Using the first and second nearest neighbour distances. Does one still
get a straight line? We could look at the mean of the first and second
nearest neighbour distances separately. Do we get a straight line
for one but not the other as you vary
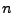 ? We can then repeat the
experiments using shuffle rather than Euclidean distance.
? We can then repeat the
experiments using shuffle rather than Euclidean distance.
- Now try the effect of varying the dimensionality. Stick to the same
sort of generating distributions, and see if you can the straight-line
behaviour for higher
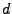 as well.
as well.
- Try with some non-Gaussian distributions. I mean some sort of bent
banana-shaped scatter, rather than anything like a flat distribution.



Next: Results
Up: Normalisation Experiments: Planning, Deployment,
Previous: Normalisation Experiments: Planning, Deployment,
Roy Schestowitz
2007-03-11
 PDF version of this entire document
PDF version of this entire document