Experimental Framework

The framework constructed over the first couple of months can be seen in Figure $[*]$ .

**Figure:** Program steps broken down into an overview-type flowchart

For the time being we concentrate on PCA and not GMDS. The key part is about PCA [], which MATLAB implements with http://www.mathworks.com/help/toolbox/stats/princomp.htmlprincomp; it is essential for constructing statistical models, via decomposition of face characteristics as derived automatically from the dataset.

**Figure:** Areplotted block diagram of the components in the IJCV paper [1] and our proposed extension/modifications (bottom), and the already-implemented procedures

Shown in Figure $[*]$ is an annotated version of the original figure from the paper. The overview is simplistic in the interests of abstraction and elegance. The graphical user interface of the program we built looked like Figure $[*]$ about a year ago (there have been many feature enhancements since).

**Figure:** Early prototype of the GUI

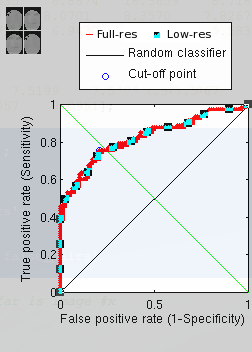
Using the PCA-based approach, we were initially able to get results of reasonable standard. Figure $[*]$ shows the ROC curve that accounts for hundreds of image pairs from the FRGC dataset.

**Figure:** ROC curve showing the PCA-based approach with its performance on 120 image pairs

In a separate experiment, the images were downsampled by a factor of 10 along each dimension, lowering by two orders of magnitude the Z axis data that gets sampled by PCA based on a grid. This ought to have kept the models more manageable for the purpose of algorithm/performance testing. Interestingly enough, downsampling hardly affected the ability to recognise faces. As Figure $[*]$ shows, the classification remained almost the same, even though the images were tiny (see Figure $[*]$ at the top left).

**Figure:** The results from full-resolution image sets and low-resolution equivalents (as seen at the top left)

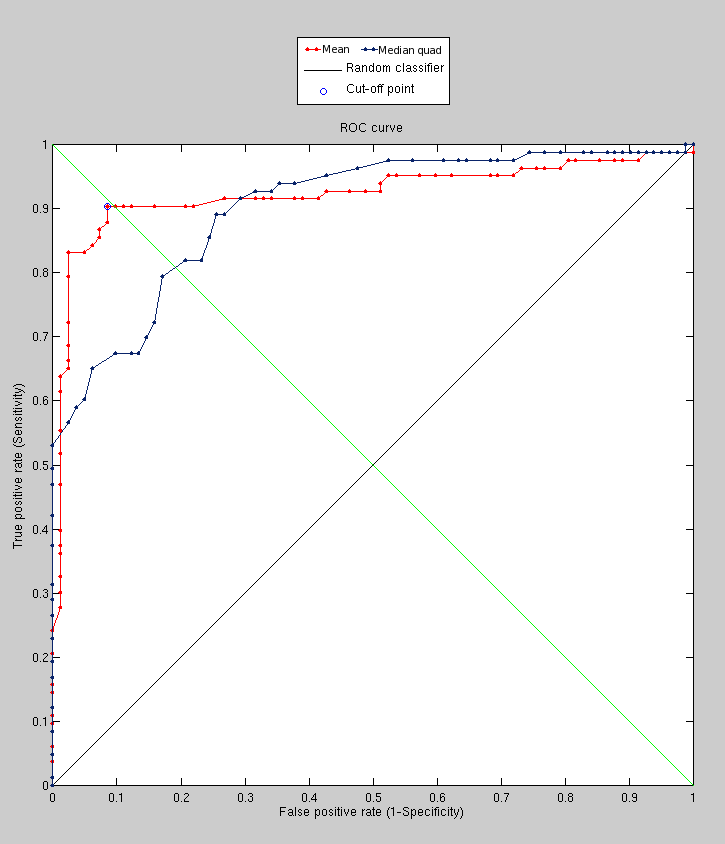
Using the same data and preprocessing as before (for the sake of a sound comparison), we have applied a PCA-based approach to get the following results, which are clearly by far superior. The variation incurred by expression is detected by PCA in the sense that it is not seen as a new type of variation.

**Figure:** The FP analysis of the results of a model-based approach, with the breakdown of modes shown at the top right

The performance, as shown in Figure $[*]$ , is therefore greatly improved and there is room for further improvements as this implementation uses tiny images to save time and it does not use the sophisticated approaches partly implemented by now.

**Figure:** Performance comparison between an approach where the median of squared differences gets compared to mean of model changes

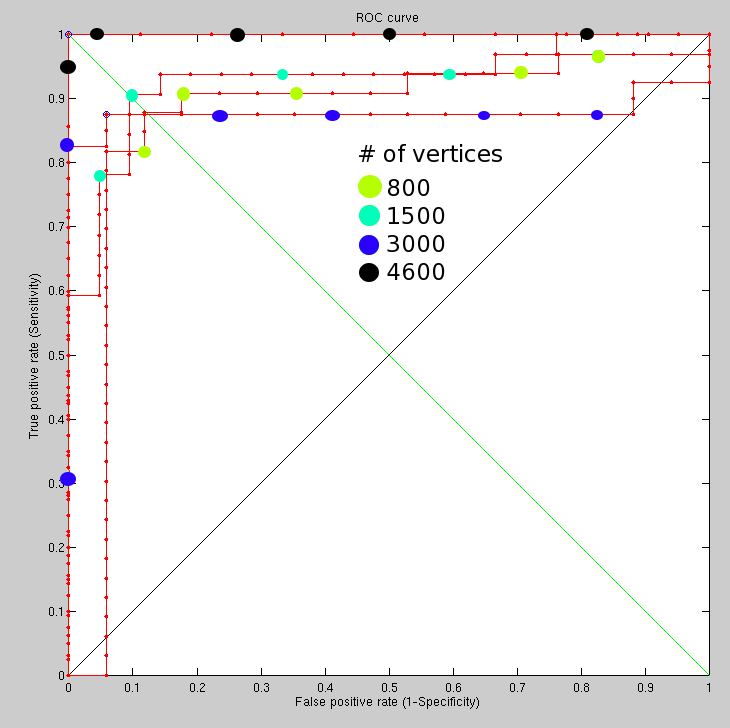
Using GMDS, the recognition performance reached at the early stages was around 90%. There were limitations related to image resolution and algorithms whose performance does not degrade linearly. These experiments took a long time to set up and run (manually) because of some freezing and stability issues at a resolution which translates to 4,600 vertices. The combination with C++ code for stress minimisation improved speed. The ROC curves in Figure $[*]$ helps show the impact of the number of vertices on performance.

**Figure:** A set of verification results obtained by systematically varying the number of vertices used

Areas of mismatch have been studied more closely in order to understand what causes them. Several large images were looked at along with the GUI (with previews of images enabled), showing quite clearly that we must remove hair from the surfaces as many mis-detections are caused by this. The aim is to get close to 99% recognition rate. The sample size is not large enough for an sufficiently informative ROC curve, but there are only a few wrong classifications. One is a borderline case where pairs from different people almost seem like belonging to the same person. The other case is mostly a case of GMDS not working, not quite a wrong classification. At all resolutions attempted so far, one pair of faces (same person imaged) cannot be made correspondent. Other than that, there is almost an order of magnitude apart in terms of separation between correct pairs and incorrect pairs. One important issue to tackle is the rare case where GMDS hardly latches onto facial features at all, as shown in Figure $[*]$ .

**Figure:** A pair that causes GMDS to fail

A GMDS-based identity verification task, with smoothed surfaces where the resolution is increased for accuracy and for improved performance, still works rather well (room remains for improvement). In the following late experiment only one image was problematic, only slightly bordering the threshold because of pose variation on the face of it (see Figure $[*]$ ). There was only one case where GMDS failed. The ROC curve is shown in Figure $[*]$ and it is the best performance level that we reached using this method.

**Figure:** A problematic pair which is seen as too different to quality as a match

**Figure:** ROC curve based on the smoothed surfaces variant of the algorithm

That last curve was obtained by using a kernel/window 13 pixels across, moving average (horizontal and vertical). The 2-D Gaussian filter is another option.

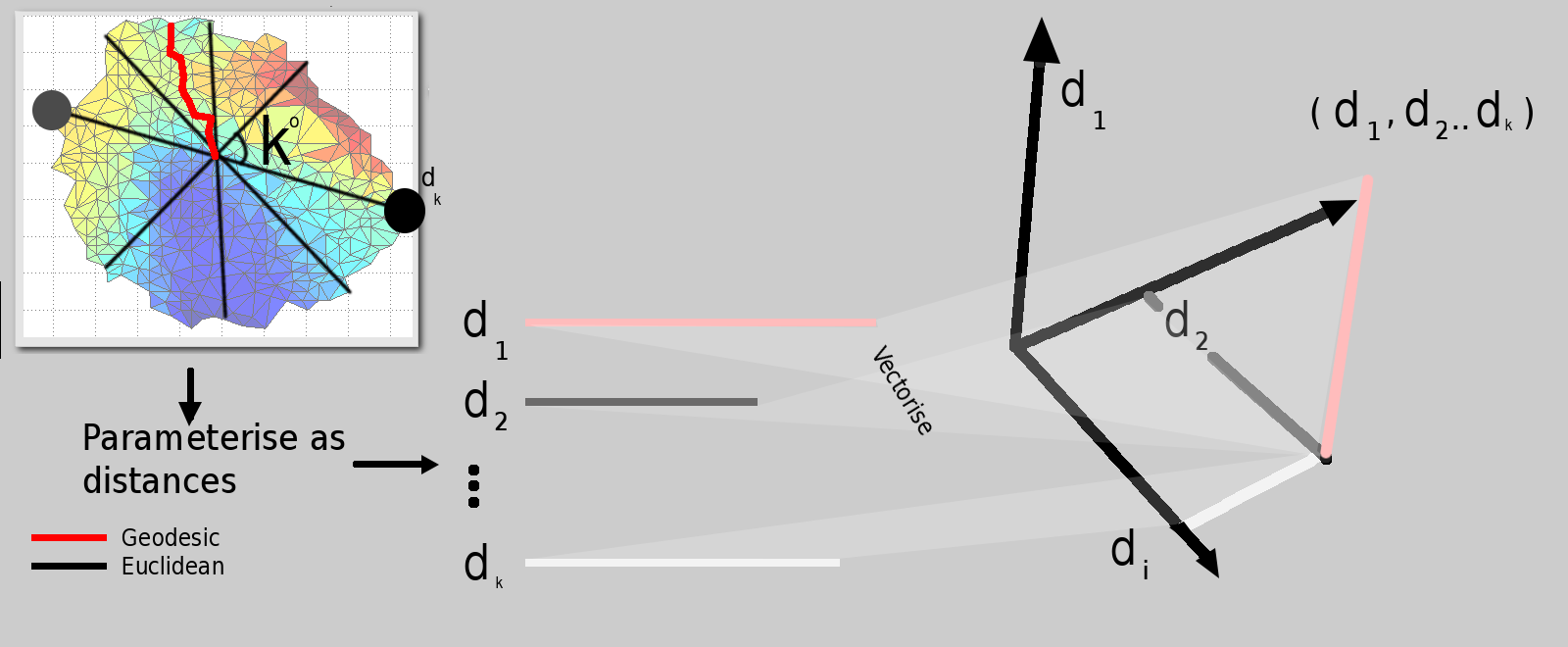
A newly-worked-on approach strives to measure distances between images in hyperspace based on their parameterised version, where these parameters are basically a small set of distances, each (hopefully) encompassing a sort of concise digital signature corresponding to a person's facial surface alone. The sketch below shows the approach. It is a brute force implementation that measures many geodesic distances and then compares surfaces based on distance-to-distance subtractions. It is not particularly clever, but the results of recognition tests are not too bad, either. They help validate the premise that by measuring Euclidean distances in XY, YZ, and XZ (based upon geodesic operators like FMM) we are able to carve out the surfaces and extract meaningful measures from the sub-surfaces.

**Figure:** Brute force implementation that measures many geodesic distances

**Figure:** This figure visualises the idea of encoding surfaces as a vector not of surface vertices but an ordered list of Euclidean-upon-geodesic distances, which are fast to compute and sensitive to isometric/mildly detectable alterations

**Figure:** Separability testing in hyperspace

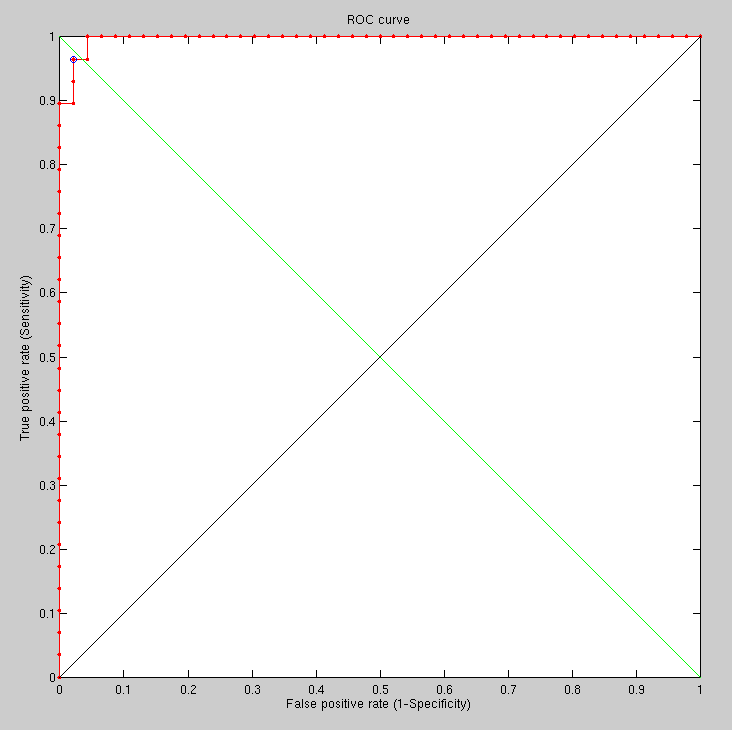
Taking the first imaged individual vs different imaged individuals (92 different individuals), the following results are obtained using the new method, which was refined and adjusted to the task at hand (Figure $[*]$ ), unlike GMDS which is generic and adaptable.

**Figure:** ROC curve obtained by measuring geodesic-Euclidean distances on the first imaged individual vs the same on different individuals

**Figure:** The result of running the test set further (not for comparative purposes)

We are able to see slight improvement incurred by the use of smoothing in the new FMM-based method. It makes sense to do this around the eyes, but currently the filter is applied uniformly to the entire image. At present, GMDS continues to show potential (more so than PCA), but its performance falls short of the modified algorithm detailed above.

**Figure:** Example of correct matching between pairs of faces, where geodesic distances are being used to carve out a subsurface for each face