PDF version of this document

Transformations

Image registration ordinarily involves the manipulation of image pixels according to some rules and under the imposition of several strict constraints. It is usually desirable to obtain a maximum similarity measure amongst a group of images with a minimal extent of distortion. Even a small level of distortion may induce wrong assumptions or violate some stern conditions which should otherwise be an unbreakable prerequisite. It is possible to think of the transformations used as if they pertain to different levels of ``interference'' - the interference to the analysis and interference with the integrity of the data. A typical categorisation of transformation types is as follows (ordered by increasing interference)²⁰:

Rigid

Allows scaling (uniformal size changes, i.e. shrinkage and enlargement), translation (location in space) and rotation. The normalised shape attributes are altogether preserved and the process is usually concerned merely with some common alignment and bias-neutralisation. Such alignment usually aims to place all instances upright and centred in the space origin with a fixed size of maximum 1 unit. The instance is virtually confined to lie inside a bounding structure (a square, or sphere in 2-D and 3-D respectively)²¹. In 3-D, for instance, there is a total of 6 degrees of freedom so a rigid transformation will be wholly characterised by a tuple of 6 values²².

Affine

Allows the instance (image) to stretch along at least one axis or dimension, but not necessarily all (so that homogeneous scaling can be broken). Despite the fact that previously essential constraints are broken, all lines that were parallel remain parallel after the transformation is applied²³. Reconstruction is said to be possible so that this transformation is invertible. For all affine transformations $T_{a}(x)$ where $x$ can be a vector representation of an image (or volume) and their inverse 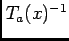$T_{a}(x)^{-1}$, the expression 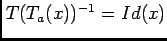$T(T_{a}(x))^{-1}=Id(x)$ must hold. This relation must always be calculable and retain simplicity which makes it easy to resolve. This will prove to be an important constraint when the practicability of warps is debated.

Non-rigid

All other valid transformations fall into this category. This includes tapering, spiral warps, pinching, etc. In principle, no inviolable constraints are in place, but quite clearly the transformation attempts to preserve some of the primary structure²⁴ of the image while avoiding tearing and folding [27]. This means that each pixel in the range must map to another and no pixel is left undefined. A bit more on this is to be explained later.

The image below illustrates the effect that each transformation is allowed to have on the image on the left.

Figure 5: Registration examples; from top to bottom: rigid, affine and non-rigid registration.

As the figure suggests, the appearance of an object remains identical under rigid transformations. It is allowed strictly to grow, shrink, move, and rotate. Affine transformation allows an object to lose its original form and non-rigid registration is far more permissive so the object can be subjected to rather obscure deformations.

What follows in this section briefly explains some of the main concepts, techniques and ideas currently devised. The actual key points, which describe non-rigid registration in the context of the Structure and Function Grand Challenge²⁵, are as follows:

1. Warps
2. Similarity
3. Objective function

These three points will be explained in a bit more detail with reference to current work, practical considerations and attempts made. For now, a concise introduction would do. The approach often taken is that an image need to be warped (equivalent to transformation) until it matches another. The match is estimated with the assistance of similarity measures and this process of warping and similarity is sometimes wrapped up and put under one generic objective function. The objective function is then handled by a general optimiser - a term which is further explained in Subsection 3.7.