PDF version of this document

Methodology

In order to measure the quality of a model, a measure was devised which reflects on its occupancy in a high-dimensional space. The method measures how well one cloud of points fits another. One cloud comprises the training set of the model whereas the other accommodates many model syntheses. A similar approach was used to evaluate shape models, thereby building optimal models of shape automatically.

The measures are based on distances between examples in two groups of instances. The first of these measures, namely specificity, is intended to discover how well a model describes its training set. The other - generalisation ability, indicates how closely the training set fits within the model. To represent the model, many synthetic instances need to be generated from it. The safe assumption is that a large enough number of instances is capable of approximating the model's behaviour.

Fig. 3. The model evaluation framework. Each image in the training set is compared against all model-generated syntheses

The shuffle transform is a robust filter that can measure difference between images that have localised discrepancies. Shuffling was used to derive images which are reminiscent of the originals, but highlighted regions of inconsistency.

Shuffle distance is defined to be the minimum value for every pixel with respect to a group of pixels in its vicinity in a second image (see Fig. 4).

Fig. XXX. Varying number of warps are applied to the training set of a model whose specificity is then evaluated using Euclidean distance and shuffle distance with varying window sizes.

           

Fig. 4. Illustrating the essence           Fig. 5. An example of the shuffle

of a shuffle distance image                  distance image when applied to two brains

To calculate 'distance' between two images, the me an intensity of the resulting shuffle distance image should be taken. This simple idea has proven to be fast, as well as powerful.

Let $\{ I_{a}(X_{0})\,:\, a\,=\,1,...\eta\}$ be a large image set which has been generated from the model and has the same distribution as the model. The distance between two images is described by $\vert\cdot\vert$ and this allows us to define:

Generalisation ability: $G=\frac{1}{N}\begin{array}{c} N\\ \sum\\ i=1\end{array}min_{\,(w.r.t.\:\, a)}\,(\vert I_{\tau_{i}}(X_{0})-I_{a}(X_{0)}\vert),$
Specificity: $S=\frac{1}{\eta}\begin{array}{c} \eta\\ \sum\\ i=1\end{array}min_{\,(w.r.t.\,\, i)}\,(\vert I_{\tau_{i}}(X_{0})-I_{a}(X_{0)}\vert)$.

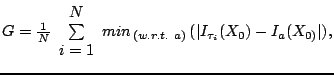
Algorithmically, a method can then be devised for evaluating models. It is based on generalisation ability and specificity and it consists of the following steps:

width

• Generate a set of model syntheses ($I_{syn}$)
• For all images in the training set ($I_{model}$):
  • Pre-process the image if necessary, e.g. resize, crop
  • For all image generated from the model:
    • Pre-process the image if necessary
    • Calculate the shuffle distance between $I_{syn}$ and $I_{model}$ and record it in an appropriate location of a matrix of size $I_{syn}\times I_{model}$
• Using the equations above, derive specificity and generalisation ability from the matrix
  
  width