 PDF version of this document
PDF version of this document
Our approach to the assessment of NRR relies on the close
relationship between registration and statistical model building,
and extends the work of Davies et al. on evaluating shape models [6].
We note that NRR of a set of images establishes the dense correspondence
which is required to build a combined appearance model. Given the
correct correspondence, the model provides a concise description of
the training set. As the correspondence is degraded, the model also
degrades in terms of its ability to reconstruct images of the same
class, not in the training set (Generalisation), and its ability to
only synthesise new images similar to those in the training set (Specificity).
If we represent training images and those synthesised by the model
as points in a high dimensional space, the clouds represented by training
and synthetic images ideally overlap fully (see Fig. 2). Given a measure
of the distance between images (see next section), Specificity, ![]() ,
Generalisation,
,
Generalisation, ![]() , and their standard errors
, and their standard errors
![]() and
and
![]() can be defined as follows:
can be defined as follows:
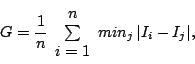 |
(5) |
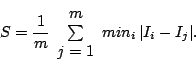 |
(6) |
| (7) |
| (8) |
where {
![]() is a large set of images sampled
from the model,
is a large set of images sampled
from the model, ![]() is the distance between two images and
SD is standard deviation.
is the distance between two images and
SD is standard deviation.
Both values are low for a good model. Specificity measures the mean distance between images generated by the model and their closest neighbours in the training set, whilst Generalisation measures the mean distance between images in the training set and their closest neighbours in the synthesised set. The approach is illustrated diagrammatically in Fig. 3.
Fig. 3. The model evaluation framework. Fig. 2. Training set and model
Each image in the training set is compared synthesis in hyperspace
against every image generated by the model