


Next: Specificity
Up: Appearance Model Evaluation
Previous: Appearance Model Evaluation
The Generalisation ability of a generative appearance model
measures the extent to which it is able to represent images of the
modelled class both seen (in the training set) and unseen (not in
the training set). A model that comprehensively captures the
variation in the modelled class should generate a distribution of
images that overlaps the training distribution as completely as
possible. This means that, if we generate a large set of synthetic
images,
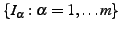 , from the model,
each image in the training set should be close to a synthetic
image. Given a measure,
, from the model,
each image in the training set should be close to a synthetic
image. Given a measure,  , of the distance between images,
we define the Generalisation
, of the distance between images,
we define the Generalisation 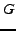 of a model and its standard
error,
of a model and its standard
error, 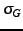 , as follows:
, as follows:
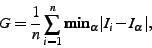 |
(3) |
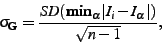 |
(4) |
where 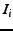 is the
is the 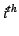 training image,
training image,
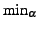 is the minimum over
is the minimum over 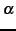 (the set of synthetic images), and SD is standard deviation. That is,
Generalisation is the average distance from each training image to
its nearest neighbour in the synthetic image set. A good model
exhibits a low value of Generalisation, indicating that the
modelled class is well-represented by the model.
(the set of synthetic images), and SD is standard deviation. That is,
Generalisation is the average distance from each training image to
its nearest neighbour in the synthetic image set. A good model
exhibits a low value of Generalisation, indicating that the
modelled class is well-represented by the model.



Next: Specificity
Up: Appearance Model Evaluation
Previous: Appearance Model Evaluation
Roy Schestowitz
2007-03-11
 PDF version of this entire document
PDF version of this entire document
![]() is the
is the ![]() training image,
training image,
![]() is the minimum over
is the minimum over ![]() (the set of synthetic images), and SD is standard deviation. That is,
Generalisation is the average distance from each training image to
its nearest neighbour in the synthetic image set. A good model
exhibits a low value of Generalisation, indicating that the
modelled class is well-represented by the model.
(the set of synthetic images), and SD is standard deviation. That is,
Generalisation is the average distance from each training image to
its nearest neighbour in the synthetic image set. A good model
exhibits a low value of Generalisation, indicating that the
modelled class is well-represented by the model.