PDF version of this entire document

A Generic Method for
Evaluating Appearance Models

R. S. Schestowitz, C. J. Twining, T. F. Cootes, V. S. Petrovic, and C. J. Taylor

Imaging Science and Biomedical Engineering, Stopford Building,
University of Manchester, Oxford Road, Manchester M13 9PT, UK.

Abstract:

Generative models of appearance have been studied extensively as a basis for image interpretation by synthesis. Typically, these models are statistical, learnt from sets of training images. Different methods of representation and training have been proposed, but little attention has been paid to evaluating the resulting models. We propose a method of evaluation that is independent of the form of model, relying only on the generative property. The evaluation is based on measures of model specificity and model generalisation ability. These are calculated from sets of distances between synthetic images generated by the model and those in the training set. We have validated the approach using Active Appearance Models (AAMs) of brain images, showing that both measures worsen monotonically as the models are progressively degraded. Finally, we compare three distinct automatic methods of constructing appearance models, and find that we can detect significant differences between them.

Interpretation by synthesis has become a popular approach to image interpretation, because it provides a systematic framework for applying rich knowledge of the problem domain. Many generative models of appearance are statistical in nature, derived from sets of training images. Active Appearance Models (AAMs) use models that are linear in both shape and texture. Their construction relies on finding a dense correspondence between images in the training set, which can be based on manual annotation or on an automated approach.

We propose a method for evaluating appearance models, that uses just the training set and the model to be evaluated. Our approach is to measure, directly, the similarity between the distribution of images generated by the model, and the distribution of training images (see Figure 1 on the left).

Figure 1: Left: A simplified representation of the model evaluation approach; Right: Calculating the shuffle difference image;

We define two measures: specificity and generalisation ability. The Generalisation ability of a generative appearance model measures the extent to which it is able to represent images of the modelled class both seen (in the training set) and unseen (not in the training set). A model that comprehensively captures the variation in the modelled class should generate a distribution of images that overlaps the training distribution as completely as possible. This means that, if we generate a large set of synthetic images, $\{I_{\alpha}:\alpha=1,\ldots m\}$, from the model, each image in the training set should be close to a synthetic image. Given a measure, $\vert\cdot\vert$, of the distance between images, we define the Generalisation $G$ of a model and its standard error, $\sigma_{G}$, as follows:

$$G=\frac{1}{n} \sum\limits_{i=1}^{n}{\bf min}_{\alpha}\vert I... ...SD({\bf min}_{\alpha}\vert I_{i}-I_{\alpha}\vert)}{\sqrt{n-1}},$$ (1)

where $I_{i}$ is the $i^{th}$ training image, $\min_{\alpha}$ is the minimum over $\alpha$ (the set of synthetic images), and SD is standard deviation. That is, Generalisation is the average distance from each training image to its nearest neighbour in the synthetic image set. A good model exhibits a low value of Generalisation, indicating that the modelled class is well-represented by the model.

The Specificity of a generative appearance model measures the extent to which images generated by the model are similar to those in the training set. We define the Specificity, $S$, and its standard error, $\sigma_{S}$, as follows:

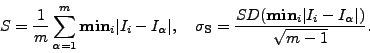$$S=\frac{1}{m} \sum\limits_{\alpha=1}^{m}{\bf min}_{i}\vert I... ...rac{SD({\bf min}_{i}\vert I_{i}-I_{\alpha}\vert)}{\sqrt{m-1}}.$$ (2)

That is, Specificity is the average distance from each synthetic image to the nearest training image. A good model exhibits a low value of Specificity, indicating that it generates synthetic images, all of which are similar to those in the training set.

To measure image distances we consider a `shuffle distance'. The idea is to seek correspondence with a wider area around each pixel. Instead of taking the mean absolute difference between exactly corresponding pixels (Euclidean distance), we take each pixel in one image in turn, and compute the minimum absolute difference between it and pixels in a shuffle neighbourhood of the exactly corresponding pixel in the other image to produce a shuffle difference image $\bigtriangleup S$ (see Figure 1 on the right).

We conducted a validation experiment whose purpose was to establish if our measures of Specificity and Generalisation were able to detect a known model degradation. The test set consisted of equivalent 2D mid-brain T1-weighted slices obtained from 3D MR scans of 36 subjects. In each of the images, a fixed number (167) of landmark points were positioned manually on key anatomical structures (cortical surface, ventricles, caudate nucleus and lentiform nucleus), and used to establish a ground-truth dense correspondence over the entire set of images, using locally-affine interpolation.

Keeping the shape vectors defined by the landmark locations fixed, smooth pseudo-random spatial warps, based on biharmonic Clamped Plate Splines (CPS) were then applied to the training images. By increasing the warp magnitude, successively-increasing mis-registration was achieved. The mis-registered training images were used to construct degraded versions of the original model. Models degraded using a range of values of the mean pixel displacement (from the correct registration) were evaluated using Specificity and Generalisation. Results are shown in Figure 2. As expected, Specificity and Generalisation both degrade (increase in value) as the mis-registration is progressively increased.

Figure 2: Specificity and Generalisation of degraded brain models.

We used our new method to evaluate three different models built using an enlarged set of the brain data containing 104 affine aligned images. We built three models, one using the pairwise approach, and two variants of our groupwise approach. The results demonstrate a clear advantage in terms of both Specificity and Generalisation for both groupwise methods over the pairwise approach.

We have introduced an objective method of assessing appearance models, that depends only on the model to be tested and the training data from which it was generated. We believe that this work makes a valuable contribution, by providing an objective basis for comparing different methods of constructing generative models of appearance.