PDF version of this entire document

Obtaining Modes of Variance

We now have our mean shape, and the set of training shapes within a common representation.

The variation of shapes is typically described in terms of variation about the mean shape; specifically, how the landmark points vary about their mean position, and how the movements of individual landmark points are correlated across a shape.

In order to learn how the positions of landmark points vary, one can perform Principal Component Analysis (PCA). In PCA, eigen analysis is used to discover the modes of variation that best describe the variation seen across the set of shapes. These shapes, which lie in a common frame of reference and are each represented by a vector, can be thought of as points in a high-dimensional space (see Figure ). What is required is a set of vectors/axes in this space that best describe the subspace in which the shape data lies. PCA provides this by extracting the eigenvectors and eigenvalues of the covariance matrix of the data set. By definition, for a column vector

$$X=\begin{array}{c} X_{1}\\ \vdots\\ X_{n}\end{array}$$

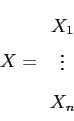
where the entries are all random variables, each with a finite variance, the following is the covariance matrix, $\Sigma$, whose $(i,j)$ entry is the covariance

$$\Sigma_{ij}=cov(X_{i},X_{j})=E[(X_{i}-\upsilon_{i})(X_{j}-\upsilon_{j})].$$

The expected value of the $i$th entry in the vector $X$ is $\upsilon_{i}=E(X_{i})$. This means that the covariance matrix looks like the following:

$$\Sigma=\begin{array}{cccc} E[(X_{1}-\upsilon_{1})(X_{1}-\ups... ...cdots & E[(X_{n}-\upsilon_{n})(X_{n}-\upsilon_{n})]\end{array}.$$

The eigenvectors form an orthonormal set, whose importance is encoded in terms of the relative size of the associated eigenvalue.

Axes aligned with these eigenvectors then provide a new coordinate system which spans the data subspace. Shapes are now described in terms of their components relative to these PCA axes, rather than the Cartesian coordinate axes that were used initially, and these PCA axes capture the correlations between the motions of landmarks.

All correlations are not equally important, and the relative importance of the PCA components is encoded by the relative sizes of their eigenvalues.

This means that we are not required to use the entire set of PCA components, but can instead choose a restricted set, that keeps only those components that are the most significant. The process is hence lossy. That loss is being controlled, however, in the sense that one can choose the minimal amount of variation which must be accounted for^3.1. What this boils down to is the building of a model that is not only smaller in size (because we do not retain all PCA components), yet one which also encapsulates the significant modes of variation in the data, and the significant correlations between landmark positions.

Figure: The two principal components in a 2-D data scatter are indicated by the two arrows