 PDF version of this entire document
PDF version of this entire document
In order to obtain a set of corresponding points, transformation of data is needed. I repeatedly used two separate `families' of registration algorithms. The first method used sum-of-squared-differences to measure similarity, whereas the second used mutual information. In both cases, transformation was handled solely using bi-harmonic clamped-plate splines.
Although mutual information is a commonly-used similarity measure, it was not used extensively during the experiments that I conducted and shall describe in the remainder of this thesis. My personal work, which is described in this section, contributed to the establishment of a framework for building models from 2-D NRR. This becomes essential later on.
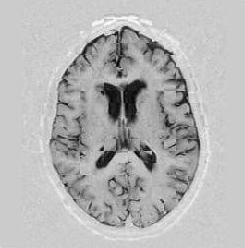
|
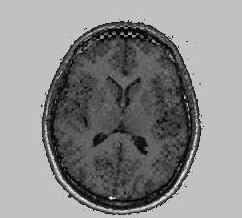
|
Figures ![[*]](/IMG/latex/crossref.png) and
and ![[*]](/IMG/latex/crossref.png) demonstrate the results of a registration process, by overlaying images
to get a mixture that is a chequerboard. What I show here is the composition
of two images, where each chequerboard position is placed adjacent
to neighboring positions (top, bottom, left and right) from another
image. If boundaries of these rectangular positions are difficult
to spot, then it is a positive sign indicating that the similarity
is high and both images are in a state of good alignment. This is
a simple way of visually examining the differences between two images
with extra attention paid to particular image regions.
demonstrate the results of a registration process, by overlaying images
to get a mixture that is a chequerboard. What I show here is the composition
of two images, where each chequerboard position is placed adjacent
to neighboring positions (top, bottom, left and right) from another
image. If boundaries of these rectangular positions are difficult
to spot, then it is a positive sign indicating that the similarity
is high and both images are in a state of good alignment. This is
a simple way of visually examining the differences between two images
with extra attention paid to particular image regions.
Roy Schestowitz 2010-04-05