PDF version of this entire document

Sensitivity

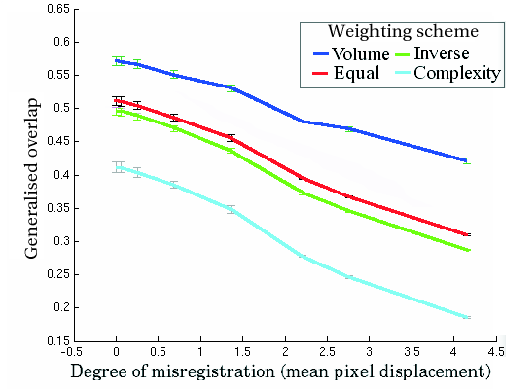
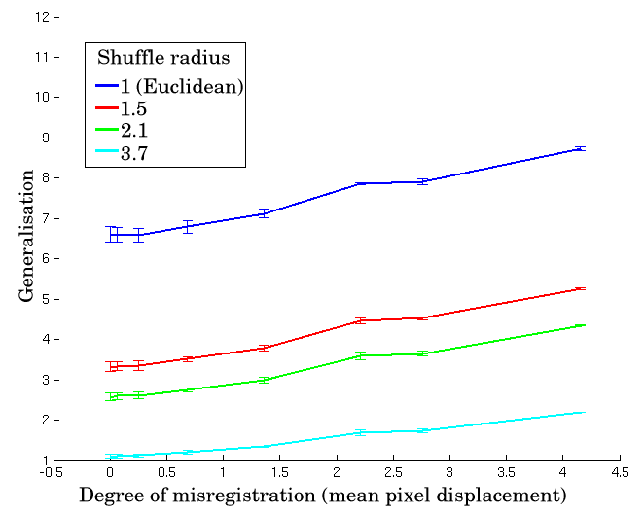
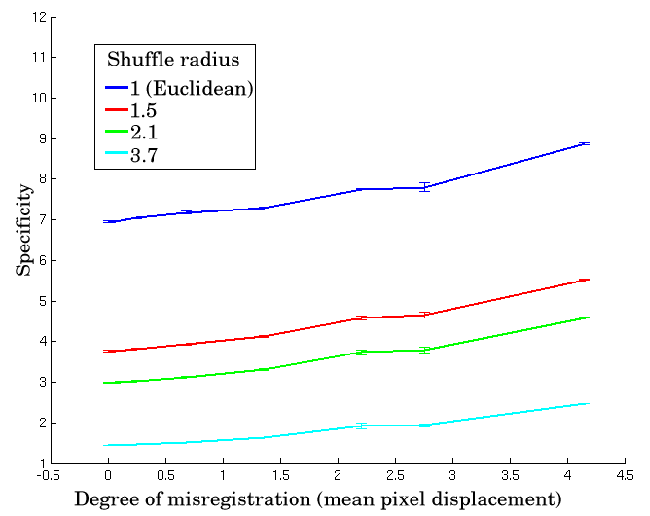
The size of perturbation that can be detected in the validation experiments will depend both on the change in the values of the measures as a function of misregistration and the standard error of those values. To quantify this, the sensitivity of a measure was defined as follows.

$$D(m;d) = \frac{1}{{\sigma}_m}\left(\frac{m(d)-m(0)}{d}\right),$$ (7.1)

where $m(d)$ is the value of the measure for some degree of deformation $d$, ${\sigma}_m$ is the standard error of the estimate of $m(d)$. $D(m;d)=1$ is the change in $d$ required for $m(d)$ to change by one noise standard error, which indicates the lower limit of change in misregistration $d$ which can be detected by the measure. $D$ is a function of $d$; to simplify comparison between different methods of evaluation, we also use the mean sensitivity over a range of values of $d$.

In order to compare the sensitivities of different methods of evaluation, the expected error in $D$ also needed to be estimated. Since the validation experiments provided repeated estimates of $m(d)$, one can obtain empirical estimates of the errors in $m(d)$, $m(0)$, and ${\sigma}_m$. These can be combined, using error propagation in Equation 7.1, to estimate the uncertainty in the estimate of sensitivity.

Figure: Overlap measures (with corresponding $\pm$ one standard error errorbars) for the MGH dataset as a function of the degree of degradation of registration correspondence, $d$. The various graphs correspond to the various tissue weightings as defined in Chapter 2.

Figure: Generalisation & Specificity for various definitions of image distance (varying shuffle radius) with corresponding $\pm$ one standard error errorbars as a function of the degree of degradation of the registration correspondence $d$ for the MGH dataset