OLLOWING this previous shoutout I was speaking to a colleague about a more reliable way of comparing two triangulated surfaces as it is required once the masking gets done and good alignment is attained.

I spent some time searching around the Web to see if someone made a robust and accurate way of doing so, rather than rely on ad hoc methods that I wrote on my own. The triangles already are reduced for analogous regions to overlap, but comparing on this basis (in 3-D) needs some cunning theory to be robust to slight changes in expression. MathWorks’ File Exchange hardly provides anything for this purpose. I looked through hundreds of submissions. There is a paper titled “Surface Matching: geodesic distance evolution PDEs on manifolds” and it links to http://www.cs.cmu.edu/~3dvision/meshtoolbox/executables.html. The page is no longer there, but there is a new working URL for it. “Overlap” is the tool closest to what we need (but not quite the best for the job). The comparison we do is not a topological one but one that should be sensitive to small localised anomalies, with just 4,000 (at most, for technical limitation in FMM) triangles. To get to the very high 90s in terms of matching rates (%-wise) I could use some advice/pointers. I have been reading “Geodesic Matching of Triangulated Surfaces”. It is a paper from A. Ben Hamza and Hamid Krim (North Carolina State University) and it demonstrates the use of Jensen-Shannon dissimilarity results. Wang et al. in “3D Brain surface matching based on geodesics and local geometry” seemed interesting and relevant. This paper, however, does not deal with surface-to-surface comparison of brains but with other problems. After a while it was time to explore older methods.

We experimented a lot with GMDS back in July until a few months later. It did not give sufficiently good results for two main reasons: 1) the separability in terms of scores was not good enough and 2) GMDS did not always find the correct correspondences, perhaps due to initialisation issues and other factors. GMDS gave recognition rates higher than 90%, but this baseline was surpassed by the newer implementation. As GMDS is a refinement mechanism, it would be useful to see what would happen if we iterate (i.e. re-run it after some other way of aligning the surfaces). I decided to give that a go.

The results so far look so-and-so, with more false pairs being run to smoothen the curve and draw better conclusions. I am merely presenting the results, irrespective of their quality, just the quality of the experiments used to arrive at them. What’s measured in this case is the best fit stress (best among all iterations), which means that the rest get altogether discarded. ~4000 triangles are used for FMM in this case.

Running further experiments to account for more example pairs has done little to actually contribute to optimism, so I will explore another approach in iterating over the set with GMDS (run overnight).

Taking the average GMDS score rather than the best fit (minimum) score leads to results that are not better. These results are significantly inferior to those attaind through the older FMM-based method.

Important enough to mention was the fact that in the aforementioned experiments — those with GMDS iterations — only the area around the nose was factored in because it surrounds the landmark point which can most accurately be determined. Experiments from last year, however, systematically showed superior performance when an estimation of eye locations form the basis for an expanded mask, so additional experiments will now be run with the expectation that they will show improved recognition performance (hopefully around 95% correct).

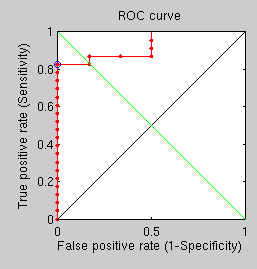
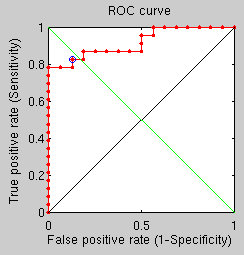
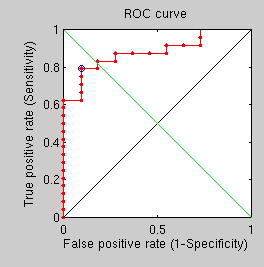
Several more experiments have been run to explore the use of GMDS in a supposedly more robust way to establish when an image pair comprises corresponding people. Starting with experiments that look at the use of 3 GMDS processes around 3 different centres, there is a best fit approach, from which the following ROC curve was obtained.

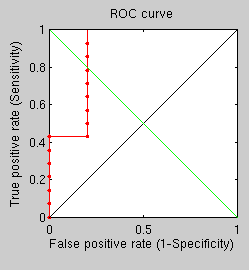
The same for average reveals similar performance.

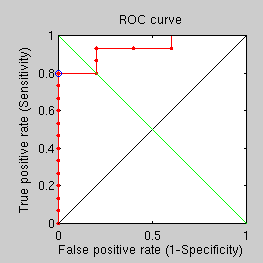
By taking all centre points at once and performing GMDS on a mask around that we get the third ROC curve.

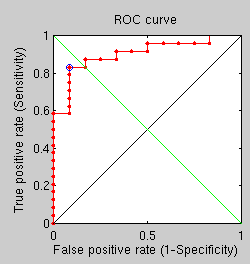
he same for average shows performance lagging considerably (in comparison with results from another approach).

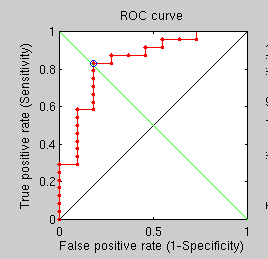
It is a lot worse than the ~97% recognition rates we got some months ago, Time to step back and rethink perhaps.

 Add your comment(s) |  Send this to a friend

This entry was posted on Sunday, January 15th, 2012 at 11:45 am and is filed under Research, Science. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.