

Next: Results
Up: Assessing the Accuracy of
Previous: Method
The overlap-based and model-based approaches were validated and
compared, using a dataset consisting of 36 transaxial mid-brain
slices, extracted at equivalent levels from a set of T1-weighted
3D MR scans of different subjects. Eight manually annotated
anatomical labels were used as the basis for the overlap method:
L/R white matter, L/R grey matter, L/R lateral ventricle, and L/R
caudate. The images were brought into alignment using an NRR
algorithm based on MDL optimisation [18]. The resulting appearance model is shown in Figure 5. A test
set of different mis-registrations was then created by applying
smooth pseudo-random spatial warps to the registered images. These warps were based on biharmonic Clamped
Plate Splines. Each warp was controlled
by 25 randomly placed knot-points, each displaced in a random
direction by a distance drawn from a Gaussian distribution whose
mean controlled the average magnitude of pixel displacement over
the whole image. Ten different warp instantiations were generated
for each image at each of seven progressively increasing values
of average pixel displacement. Registration quality was measured,
for each level of registration degradation, using several variants
of each of the proposed assessment methods.
The results of the validation experiment are shown in Figure
4. Note that 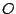 is expected to decrease with
increasing perturbation of the registration, whilst
is expected to decrease with
increasing perturbation of the registration, whilst 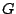 and
and 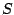 are expected to increase. All three metrics are generally
well-behaved and show a monotonic response to increasing
perturbation. This validates the model-based measures of
registration quality, which are shown both to change monotonically
with increasing perturbation of the registration and to correlate
with the gold-standard approach based on manually annotated ground
truth.
are expected to increase. All three metrics are generally
well-behaved and show a monotonic response to increasing
perturbation. This validates the model-based measures of
registration quality, which are shown both to change monotonically
with increasing perturbation of the registration and to correlate
with the gold-standard approach based on manually annotated ground
truth.
Figure 5:
The sensitivities of the different registration assessment
methods and their standard errors.
|
[width=]../EPS/BW_MIAS_sensitivity_label.png
|
The results for different values of 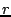 (shuffle radius) and
(shuffle radius) and
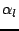 all demonstrate monotonic behaviour with increasing
perturbation, but the slopes and errors vary systematically. This
affects the size of perturbation that can be detected. To make a
quantitative comparison of the different methods, we define the
sensitivity, as a function of perturbation
all demonstrate monotonic behaviour with increasing
perturbation, but the slopes and errors vary systematically. This
affects the size of perturbation that can be detected. To make a
quantitative comparison of the different methods, we define the
sensitivity, as a function of perturbation
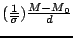 , where
, where 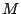 is the
quality measured for a given degree of deformation
is the
quality measured for a given degree of deformation 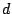 ,
, 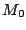 is the
measured quality at registration (no deformation)
and
is the
measured quality at registration (no deformation)
and
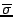 is the mean error in the estimate of
is the mean error in the estimate of 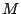 over the range.
over the range.


Next: Results
Up: Assessing the Accuracy of
Previous: Method
Roy Schestowitz
2006-02-08
 PDF version of this document
PDF version of this document
![]() is expected to decrease with
increasing perturbation of the registration, whilst
is expected to decrease with
increasing perturbation of the registration, whilst ![]() and
and ![]() are expected to increase. All three metrics are generally
well-behaved and show a monotonic response to increasing
perturbation. This validates the model-based measures of
registration quality, which are shown both to change monotonically
with increasing perturbation of the registration and to correlate
with the gold-standard approach based on manually annotated ground
truth.
are expected to increase. All three metrics are generally
well-behaved and show a monotonic response to increasing
perturbation. This validates the model-based measures of
registration quality, which are shown both to change monotonically
with increasing perturbation of the registration and to correlate
with the gold-standard approach based on manually annotated ground
truth.
![]() (shuffle radius) and
(shuffle radius) and
![]() all demonstrate monotonic behaviour with increasing
perturbation, but the slopes and errors vary systematically. This
affects the size of perturbation that can be detected. To make a
quantitative comparison of the different methods, we define the
sensitivity, as a function of perturbation
all demonstrate monotonic behaviour with increasing
perturbation, but the slopes and errors vary systematically. This
affects the size of perturbation that can be detected. To make a
quantitative comparison of the different methods, we define the
sensitivity, as a function of perturbation
![]() , where
, where ![]() is the
quality measured for a given degree of deformation
is the
quality measured for a given degree of deformation ![]() ,
, ![]() is the
measured quality at registration (no deformation)
and
is the
measured quality at registration (no deformation)
and
![]() is the mean error in the estimate of
is the mean error in the estimate of ![]() over the range.
over the range.