


Next: Measuring Image Separation
Up: Model-Based Evaluation of NRR
Previous: Model-Based Evaluation of NRR
A good model of a set of training data should possess several
properties. Firstly, the model should be able to extrapolate and
interpolate effectively from the training data, to produce a range
of images from the same general class as those seen in the
training set. We will call this generalisation ability.
Conversely, the model should not produce images which cannot be
considered as valid examples of the class of object imaged. That
is, a model built from brain images should only generate images
which could be considered as valid images of possible brains. We
will call this the specificity of the model. In previous
work, quantitative measures of specificity and generalisation were used to evaluate shape models [17].
We present here the extension of these ideas to
images (as opposed to shapes). Figure 2 provides an
overview of the approach.
Consider first the training data for the model, that is, the set
of images which were the input to NRR. Without loss
of generality, each training image can be considered as a single
point in an 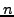 -dimensional image space. A statistical model is
then a probability density function
-dimensional image space. A statistical model is
then a probability density function
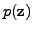 defined on this
space.
defined on this
space.
Figure 2:
The model
evaluation framework: A model is constructed from the training set
and then used to generate synthetic images. The training set and
the set generated by the model can be viewed as clouds
of points in image space.
|
|
To be specific, let
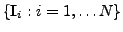 denote the
denote the 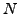 images
of the training set when considered as points in image space. Let
images
of the training set when considered as points in image space. Let
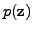 be the probability density function of the model.
We define a quantitative measure of the specificity
be the probability density function of the model.
We define a quantitative measure of the specificity 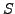 of
the model with respect to the training set
of
the model with respect to the training set
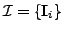 as follows:
as follows:
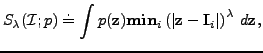 |
(8) |
where  is a distance on image space, raised to some
positive power
is a distance on image space, raised to some
positive power 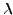 . That is, for each point
. That is, for each point
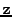 on image
space, we find the nearest-neighbour to this point in the training
set, and sum the powers of the nearest-neighbour distances,
weighted by the pdf
on image
space, we find the nearest-neighbour to this point in the training
set, and sum the powers of the nearest-neighbour distances,
weighted by the pdf
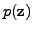 . Greater specificity is
indicated by smaller values of
. Greater specificity is
indicated by smaller values of 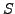 , and vice versa. In
Figure 3, we give diagrammatic examples of models with
varying specificity.
, and vice versa. In
Figure 3, we give diagrammatic examples of models with
varying specificity.
The integral in equation 6 is approximated using a Monte-Carlo method. A large
random set of images
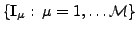 is
generated, having the same distribution as the model pdf
is
generated, having the same distribution as the model pdf
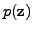 .
The estimate of the specificity (6) is:
.
The estimate of the specificity (6) is:
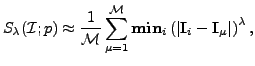 |
(9) |
with standard error:
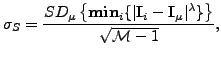 |
(10) |
where 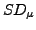 is the standard deviation of the set of
is the standard deviation of the set of
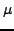 measurements.
measurements.
Figure 3:
Training set (points) and model pdf
(shading) in image space. Left: A model
which is specific, but not general. Right:
A model which is general, but not specific.
|
|
A measure of generalisation is defined similarly:
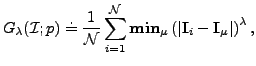 |
(11) |
with standard error:
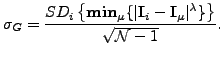 |
(12) |
That is, for each member of the training set
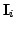 , we compute the distance to the
nearest-neighbour in the sample set
, we compute the distance to the
nearest-neighbour in the sample set
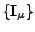 .
Large values of
.
Large values of 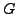 correspond to model
distributions which do not cover the training set
and have poor generalisation ability, whereas
small values of
correspond to model
distributions which do not cover the training set
and have poor generalisation ability, whereas
small values of 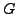 indicate models
with better generalisation ability.
indicate models
with better generalisation ability.
We note here that both measures can be further extended, by
considering the sum of distances to k-nearest-neighbours, rather
than just to the single nearest-neighbour. However, the choice of
k would require careful consideration and in what follows, we
restrict ourselves to the single nearest-neighbour case.



Next: Measuring Image Separation
Up: Model-Based Evaluation of NRR
Previous: Model-Based Evaluation of NRR
Roy Schestowitz
2007-03-11
 PDF version of this entire document
PDF version of this entire document
![]() -dimensional image space. A statistical model is
then a probability density function
-dimensional image space. A statistical model is
then a probability density function
![]() defined on this
space.
defined on this
space.
![]() denote the
denote the ![]() images
of the training set when considered as points in image space. Let
images
of the training set when considered as points in image space. Let
![]() be the probability density function of the model.
We define a quantitative measure of the specificity
be the probability density function of the model.
We define a quantitative measure of the specificity ![]() of
the model with respect to the training set
of
the model with respect to the training set
![]() as follows:
as follows:
![]() is
generated, having the same distribution as the model pdf
is
generated, having the same distribution as the model pdf
![]() .
The estimate of the specificity (6) is:
.
The estimate of the specificity (6) is: