PDF version of this entire document

Combined Models

The models in Equation and Equation have a linear form, so they are quite compact. This is a highly desirable property which makes the models flexible and manageable.

However, at the moment, the two components of the model, namely the shape $\mathbf{x}$ and the shape-free texture $\mathbf{g}$, are independent. In real images, shape and texture are not necessarily independent. One simple example to think of is an image of an individual's face. When the person changes expression, the shape of the face changes. But the texture (i.e. positions of highlights and shadows) obviously changes too, in a way that is correlated with the shape change. Hence it is desirable to merge the shape and texture models, so as to obtain a new model that is aware of both types of variation. This combined model can then also incorporate any correlations between shape and texture.

The parameters $\mathbf{b}_{s}$ and $\mathbf{b}_{g}$ are aggregated to form a single column vector

$$\left\{ \begin{array}{cc} \mathbf{b}_{s}\\ \mathbf{b}_{g}\end{array}\right\} .$$ (3.6)

The new vector is a simple concatenation of the two. However, since the values of intensity and shape can be very different in magnitude, weighting is needed. Such weighting brings equilibrium, under which both shape and intensity maintain a sufficiently-noticeable effect and impact on the model they jointly build. A weighing matrix resolves the problem introduced here and it is, by convention, named $\mathbf{W}_{s}$^3.4. With weighing in place, aggregation takes the form

$$\left\{ \begin{array}{cc} \mathbf{\mathbf{W}_{\mathbf{\mathbf{s}}}}\mathbf{b}_{s}\\ \mathbf{b}_{g}\end{array}\right\}$$ (3.7)

where $\mathbf{W}_{s}$ is set to minimise inconsistencies due to scale. By applying another PCA step to the aggregated data, the following combined model is obtained

$$\begin{array}{cc} \mathbf{x}_{i}=\bar{\mathbf{x}}+\mathbf{Q}... ..._{i}=\mathbf{\bar{g}}+\mathbf{Q}_{g}\mathbf{c}_{i}\end{array}.$$ (3.8)

The appearance (shape and texture) is now purely controlled by the new set of parameters, $\mathbf{c}$. There is no need to choose values for two `families' of distinct parameters. This combined model reaps the benefits of the dimensionality reduction performed, which is based on shape as well appearance. This means that this new model encompasses all the variation learned and the correlation between these two distinct components. Since PCA was applied, the number $n$ of parameters $\mathbf{c}_{i}$ is expected to be smaller than the number of parameters in $\mathbf{b}_{s}$ and $\mathbf{b}_{g}$ put together.

Figure: The effect of varying the first (top row), second, and third parameter of a brain appearance model by $\pm2.5$ standard deviations

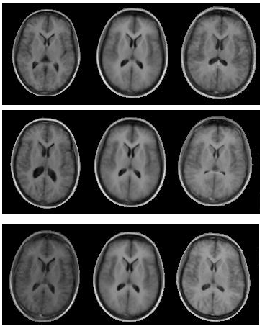
The effect of varying different elements of a combined model $\mathbf{c}$ for a model built from a set of 2-D MR brain images is shown in Figure . The number of modes (columns) in $\mathbf{Q}_{s}$ and $\mathbf{Q}_{g}$ is one less than the number of images. In practice, it is often possible to approximate images pretty well, using fewer modes $m$.