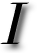N the previous post on this subject we looked at the masks used in a GMDS pipeline tailored for recognition purposes. The question now is, what would be a constructive way to progress from the conclusion?

Well, the goal is to beat the competition and do so with methods of a particular kind — the kind we advocate — which seems achievable but requires a lot of tinkering, seeing where and how mistakes can be resolved/avoided.

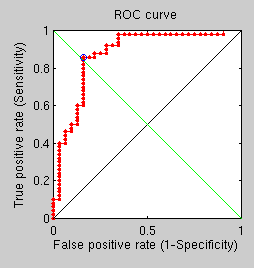
An additional experiment, taking about a day to complete, shows not much promise. Its goal is simply to compare the performance of GMDS with the new Fast Marching Methods-based measures (faster) when all parameters are kept consistent across runs. With many rings, many points, and many vertices, recongition performance is relatively poor because of the hard dataset, as demonstrated by the ROC curve. The point to note though is that in hard cases GMDS is outperformed by the other approach. One question is, are there any measurable quantifies (other than stress) resulting from GMDS and capable of assessing similarity?

GMDS multiple runs

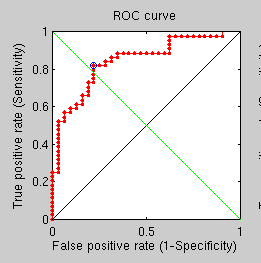
FMM-based

There are some additional results from the last set of shallow, comparative tests. By applying the same experiment’s parameters to test an antiquated triangle-counting approach and a best fit GMDS approach (rather than average over multiple runs) we get two more ROC curves.

Triangle counting

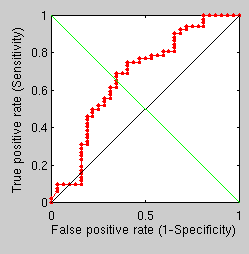
GMDS best fit

Finally, using this same difficult set (where problematic cases are included) we get a ROC curve for the standard GMDS approach.

Simple GMDS

In GMDS one could either work with and L₂ norm (which is what we do right now) or L_infty. In fact, if one takes the log of the distances and apply GMDS, one does, in a sense Lipschitz embedding. The diffusion distances could also be used within the GMDS framework. In fact, with better interpolation properties, one can interpolate the eigenfunction before integrating the distance itself…

I spoke to a colleague about L_infty and I now attempt to compile it on GNU/Linux (not done before). It would be interesting to know if GMDS been tested where D is computed based on spectral properties (not as geodesics). There an IJVC paper with Sapiro in which this is done; in it, the authors are also finding symmetries that way.

 Add your comment(s) |  Send this to a friend

This entry was posted on Wednesday, January 25th, 2012 at 11:46 pm and is filed under Research. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.