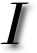 N OUR pursuit of a similarity measure for anatomical surfaces (biomedical or otherwise external to one’s body), integration over the dot product between the normals is considered. This is a powerful correlation measure between aligned surfaces, i.e. integral |<normal_1,normal_2>| delta area. The higher the integral, the higher the correlation.
N OUR pursuit of a similarity measure for anatomical surfaces (biomedical or otherwise external to one’s body), integration over the dot product between the normals is considered. This is a powerful correlation measure between aligned surfaces, i.e. integral |<normal_1,normal_2>| delta area. The higher the integral, the higher the correlation.
If we have the two surfaces given as S(x,y) and Q(x,y) and da(S) = \sqrt{S_x^2+S_y^2+1} and the normal is given by N_S(x,y) = {-S_x,-S_y,1}/da(S), then one option is: <N_S,N_q> da = (S_x*Q_x+S_y*Q_y+1)/da(Q). A more unbiased one is to integrate over: |S_x*Q_x+S_y*Q_y+1|(1/da(Q)+1/da(S)) after alignment.
Normals were explored for a while as the normals can truly be taken into account for measuring correlation between images. Here is what some noisy normals look like when scattered arbitrarily.

Normals should be better than surface area, but one should be careful with normals at the boundary, one should probably ignore them.
Surface Normals were tested for almost a week. On its own, the integral produces a similarity measure not superior to some that we already have, but it can be used to further improve classification, based on another distinct method. Fixing the ranges for the integration is the trickier bit which needs more adjustment. I have been testing some variants around this measure, but there is still lots more that can be done (this ROC curve is based on a measure applied to entire images).

If we do not eliminate outlier noise first, there would be not much use to most l2-based measures.
Apropos, this new paper [PDF] came out which suggests one other way of using geodesic distances, more robustly. In order to take better advantage of spatial properties such as surface edges (greater steepness) and alignment among normals, the placement of points for geodesic methods has become based on such properties rather than having them spread randomly or at fixed positions as before. Results will be presented in a moment.
In the case of faces, slight occlusion is a real problem for us, e.g. around the nose/nostrils, not to mention hole filling around areas like the eyes. It weakens the measures. Real geodesics or workarounds can help mitigate the inaccuracy caused by this, but really, there is lack of information in particular parts and it’s inherently a problem. By dividing the image into partitions one can get more ‘localised’ distances, still based on graph theory and the Sethian et al. approach. The results in the paper are given for 2-D+3-D and are not quite so competitive; they are tested on databases I have not come across in the literature before. To measure geodesics around anatomically analogous points (not overlapping points after ICP), I am now using edges and normals; the hard part is adjusting thresholds such that across people the same points (e.g. nose edges) can be consistently detected.
Sobel on same person:

Roberts on same person:

Canny (edge detection algorithm) on same person:

Canny applied to different persons:

Using 3-D data alone, we wish to choose anchor points for FMM which are not determined exclusively by ICP (e.g. overlapping points after alignment). I have spent several days trying to use edge detection and normals to identify points around which to extend geodesic rings. So far, the results have not been encouraging enough; in fact, they’re less promising than while relying on ICP alone. Even the placements of overlapping points at random gave much better verification results.
Canny on same person:

Canny applied to different persons (subset shown as Voronoi cells):

 oday was a great day as it was sunny, too. I left the house at 10 AM for a run around Salford and then sat down to type a few articles around a waterfall down the river (articles for Techrights of course). My knee started to hurt from all that running. I got back at 12:30 and then went cycling to a friend’s house. We cycled down the canal and stopped at the supermarket to buy some new bike kit, coal, steaks, and other meats. We then rode further till we came not so far from my house and had barbecue, then enjoyed some drinks and had chats with friends (over videophone on Android). Here are some photos from the latter part of the day. On the left side is the building I live in.
oday was a great day as it was sunny, too. I left the house at 10 AM for a run around Salford and then sat down to type a few articles around a waterfall down the river (articles for Techrights of course). My knee started to hurt from all that running. I got back at 12:30 and then went cycling to a friend’s house. We cycled down the canal and stopped at the supermarket to buy some new bike kit, coal, steaks, and other meats. We then rode further till we came not so far from my house and had barbecue, then enjoyed some drinks and had chats with friends (over videophone on Android). Here are some photos from the latter part of the day. On the left side is the building I live in.







 Filed under:
Filed under: 
 inding someone special who understands my mind is not easy. Finding someone who did the same degree as me (and is not male) is also hard, as Computer Science is largely dominated by geeky males. After many years looking for the right girl I finally found her last year. We recently got engaged, too. Here are some very recent photos.
inding someone special who understands my mind is not easy. Finding someone who did the same degree as me (and is not male) is also hard, as Computer Science is largely dominated by geeky males. After many years looking for the right girl I finally found her last year. We recently got engaged, too. Here are some very recent photos.

 ost of my life
ost of my life 







 ere he is after his hair was trimmed a bit for summer. Usually he’s all fluffy.
ere he is after his hair was trimmed a bit for summer. Usually he’s all fluffy.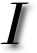 N OUR pursuit of a similarity measure for anatomical surfaces (biomedical or otherwise external to one’s body), integration over the dot product between the normals is considered. This is a powerful correlation measure between aligned surfaces, i.e. integral |<normal_1,normal_2>| delta area. The higher the integral, the higher the correlation.
N OUR pursuit of a similarity measure for anatomical surfaces (biomedical or otherwise external to one’s body), integration over the dot product between the normals is considered. This is a powerful correlation measure between aligned surfaces, i.e. integral |<normal_1,normal_2>| delta area. The higher the integral, the higher the correlation.






